The Smith Chart: Its History and Why It’s So Important for RF Designers
Novice designers doing RF design and trying to make a direct connection between two components—for example, from a voltage-controlled oscillator (VCO) to a mixer—have undoubtedly come across strange, circular graphs on component data sheets, such as these for the Maxim Integrated MAX2472, a 500-to-2500 megahertz (MHz) VCO buffer amplifier (Figure 1). These graphs, called Smith charts, are very different than anything seen in algebra or statistics classes, no doubt of that.
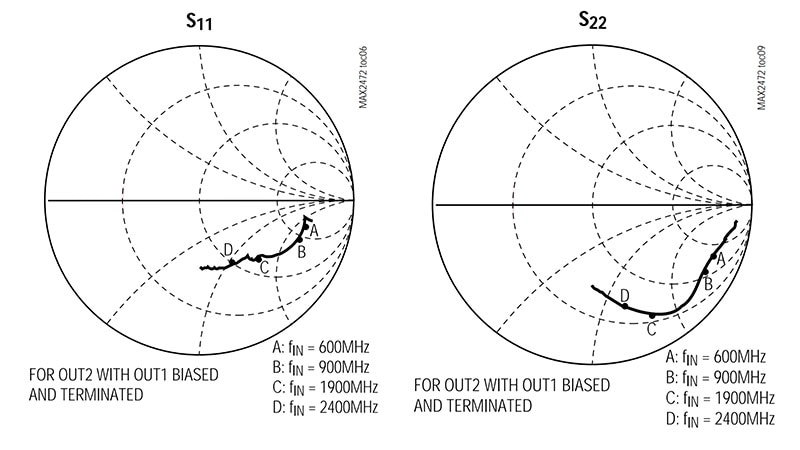 Figure 1: Many RF component data sheets include Smith charts showing the values of key parameters at different operating frequencies, such as these for the Maxim MAX2472 VCO buffer amplifier at 600, 900, 1900, and 2400 MHz. (Image source: Maxim Integrated)
Figure 1: Many RF component data sheets include Smith charts showing the values of key parameters at different operating frequencies, such as these for the Maxim MAX2472 VCO buffer amplifier at 600, 900, 1900, and 2400 MHz. (Image source: Maxim Integrated)
The chart is named for Phillip Smith, an engineer at Bell Telephone Laboratories, who devised and refined it between 1936 and 1939 while working on understanding transmission lines and standing waves at what was then considered “high frequencies” of up to 1 MHz (called megacycles per second in those days). His strange-looking circular chart has become the single most useful and powerful tool for working with and optimizing high-frequency circuits with respect to their input and output impedance, even in our age of powerful computers and computer-aided design (CAD) tools.
Among its many uses, the Smith chart provides an efficient way to visualize design options when trying to match interstage source and load impedances, a very important consideration in many circuits, especially RF design. There are two reasons such matching is critical:
• First, to realize maximum power transfer from a source to a load, the source’s complex impedance RS + jXS must equal the complex conjugate RL - jXL of the load impedance:

Where R is the resistive (real) part of the impedance and X is the reactive (inductive or capacitive) part (Figure 2).
 Figure 2: A major challenge in RF and transmission line design is ensuring that the source “sees” a load impedance, which is the complex conjugate of the source’s impedance, even if that load impedance is not there. (Image source: HandsOnRF.com)
Figure 2: A major challenge in RF and transmission line design is ensuring that the source “sees” a load impedance, which is the complex conjugate of the source’s impedance, even if that load impedance is not there. (Image source: HandsOnRF.com)
- Second, even if such power loss is not a concern (although it almost always is), impedance matching is needed to minimize the reflection of energy from the load back to the source, which can damage the source’s output circuitry.
What the Smith chart shows
The Smith chart is a polar plot of the complex reflection coefficient (also called gamma and symbolized by rho (Γ)). It succeeds at displaying what may seem at first to be an almost impossible task: the simultaneous graphing of the real and imaginary parts of a complex impedance, where the real part R can range from 0 to infinity (∞) and the imaginary part X can span minus infinity to plus infinity—and do so all on a single sheet of paper.
A simplified Smith chart, showing its circles of constant resistance and arcs of constant reactance, is a good starting point to understanding its arrangement (Figure 3). As an added benefit, the chart also provides a way to show scattering parameters (s-parameters) and how their values relate to actual hardware measurements and considerations.
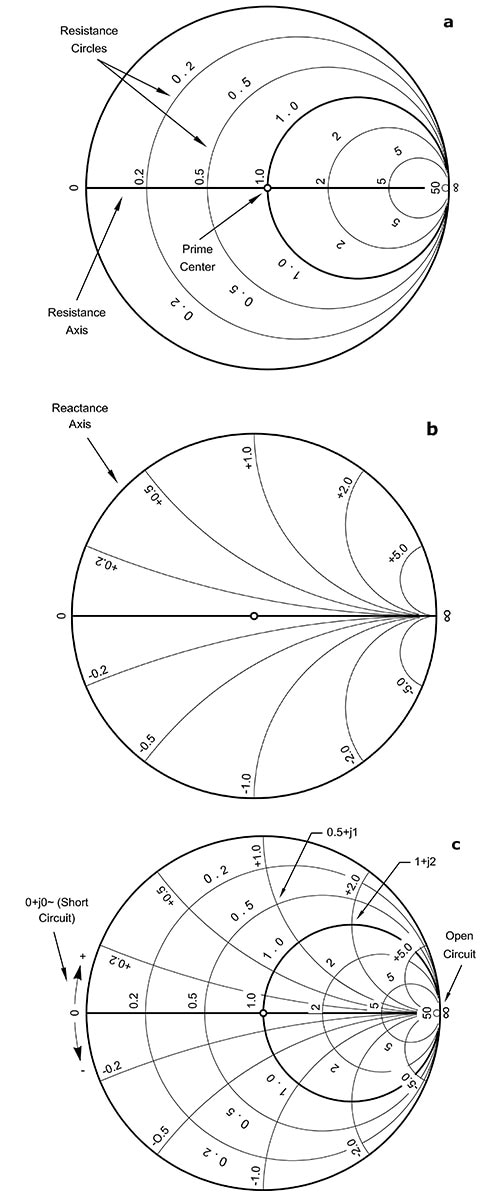 Figure 3: The Smith chart shows arcs of constant resistance (a) and circles of constant reactance (b) which are merged and overlaid (c) to provide a perspective across all impedance possibilities. (Image source: ARRL.org)
Figure 3: The Smith chart shows arcs of constant resistance (a) and circles of constant reactance (b) which are merged and overlaid (c) to provide a perspective across all impedance possibilities. (Image source: ARRL.org)
Once these complex impedance values are marked on the Smith chart, the chart can be used to identify many parameters which are critical to understanding the RF signal path or transmission line situation including:
- Complex voltage and current reflection coefficients.
- Complex voltage and current transmission coefficients.
- Power reflection and transmission coefficients.
- Reflection loss.
- Return loss.
- Standing wave loss factor.
- Maximum and minimum voltage and current, as well as standing wave ratio (SWR).
- Shape, position, and phase distribution along with voltage and current standing wave.
But that’s only a part of the power of the Smith chart. While it is useful and often necessary for designers to know the above parameters, the Smith chart can guide analysis and design decisions including:
- Display of complex impedances versus frequency.
- Display of s-parameters of a network versus frequency.
- Evaluation of input reactance or susceptance of open and shorted stubs.
- Evaluation of effects of shunt and series impedances on the impedance of a transmission line.
- For displaying and evaluating the input impedance characteristics of resonant and anti-resonant stubs, including the bandwidth and Q.
- Designing impedance-matching networks using single or multiple open or shorted stubs, quarter-wave line sections, and lumped L-C components.
The benefits of the Smith chart
At first glance, the standard, fully detailed Smith chart may look like a nearly incomprehensible jumble of lines going in all directions (Figure 4), but it is really just a higher-resolution, more detailed rendering of the simplified chart previously shown. You can download a printable version of a Smith chart from the resources in the online DigiKey Innovation Handbook.
 Figure 4: A typical Smith chart can look imposing, but it is just a higher-resolution, more detailed rendering of the simplified chart previously shown. (Image source: DigiKey)
Figure 4: A typical Smith chart can look imposing, but it is just a higher-resolution, more detailed rendering of the simplified chart previously shown. (Image source: DigiKey)
The Smith chart shows more than just a single solution to many design-related problems: it shows the many possible solutions. Designers can then decide which ones offer suitable sets of component values for the specific situation, such as practical values for impedance-matching inductors and capacitors. In most cases, the chart’s number scales are “normalized” to 50 ohm (Ω) systems, as this is the most common impedance used in RF design.
The Smith chart is so important and useful that many test instruments for RF and microwave applications, such as vector network analyzers (VNAs), can chart and display it. For example, the Teledyne LeCroy T3VNA VNA offers such a mode (Figure 5).
 Figure 5: The T3VNA vector network analyzer can display acquired data in Smith chart format. (Image source: Teledyne LeCroy)
Figure 5: The T3VNA vector network analyzer can display acquired data in Smith chart format. (Image source: Teledyne LeCroy)
How hard is it to learn to use the Smith chart? As with most such questions, it’s the same as asking different students how they feel about the difficulties of calculus or electromagnetic field theory: it depends. There are many online text and video tutorials that start with Smith chart basics then add transmission line equations and analytical perspectives. They also go through numerous examples for using it. Of course, there are also apps and programs which ease graphing, framing the problem, and evaluating options using the Smith chart. However, it helps to first understand the chart basics before resorting to these.
Conclusion
It’s amazing that a graphical tool developed over 80 years ago, long before RF design as we now know it even existed, is still one of the key resources for both paper and software-based RF design challenges. Used either way, the Smith chart is a powerful tool for displaying and assessing RF parameters, and gaining insight into design alternatives and their associated tradeoffs. The best way to learn about the power of the Smith chart and what it can do for you is to use it and work through some of the many published examples.
Recommended Reading
1 – “The Smith Chart: An ‘Ancient’ Graphical Tool Still Vital in RF Design”
2 – “SAW Filters Rescue Wireless Products from Impractical Discrete Implementations”
3 – “Understanding the Basics of Low-Noise and Power Amplifiers in Wireless Designs”
4 – “Use Log Amps to Enhance Sensitivity and Performance in Wide-Dynamic-Range RF and Optical Links”
https://www.digikey.com/en/articles/use-log-amps-to-enhance-sensitivity-logarithmic-amplifiers

Have questions or comments? Continue the conversation on TechForum, DigiKey's online community and technical resource.
Visit TechForum










