ADC 仅仅是随机数发生器吗？

ADC 有多出色呢？这个问题并不是问 ADC 的分辨率是多少；16 位 ADC 并不总是能提供有用的 16 位信息，这种说法可能会让你大吃一惊！Mike Stone 在《ADC 选型》一文中指出，许多 16 位 ADC 实际上是被用作 7 位 ADC 和 9 位随机数生成器。本文介绍如何确定 ADC 生成的随机数是否多于所需的有用随机数，以及如何减少这种随机性的几种简单方法。

我们来考虑一个简化设置：用 ADC 测量光敏电阻电压。如果图 1 中的 12 位 ADC（V_FS = 3.3 V）报告的值为 2048，那么这是否意味着光敏电阻电压为 1.65 V？

图 1：测量光敏电阻电压的简化 ADC 设置。(图片来源：Nathan Jones）

不，事实并非如此！为方便演示，可以取第二个样本，然后取第三个样本，事实上，可以取 100,000 个样本并绘制结果图。我们将看到 ADC 值的分布情况（图 2）；如果设置没有任何变化，那么其中任何一个值都可能是光敏电阻的真实电压，而最有可能的就是所有这些采样的平均值。

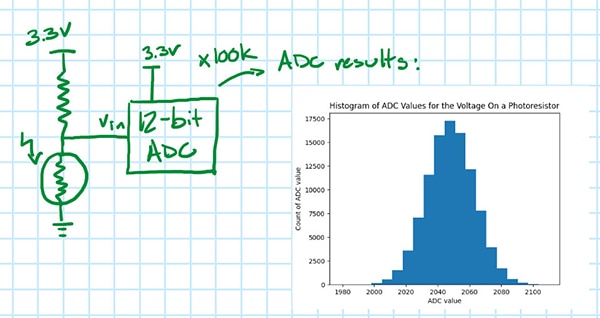图 2：其中的插图显示了 100,000 个光敏电阻电压样本的 ADC 值直方图。(图片来源：Nathan Jones）

这就引出了另一个问题。其中的一些变化会不会是输入信号的实际变化？会的。为了测试这一点，将电阻分压器换成已知噪声水平的电压基准（图 3），然后重复实验。

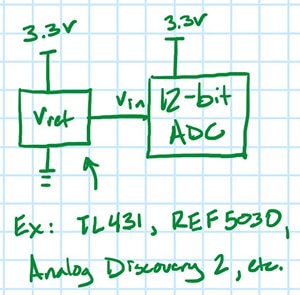图 3：用电压基准代替电阻分压器的新测试设置。(图片来源：Nathan Jones）

理想情况下，所用电压基准的噪声水平应小于 ADC 预期噪声水平的 1/3（例如，如果 ADC 的预期噪声为 ±1 LSB [使用上述示例中的 ADC 时为 ±0.8 mV]，则理想状态下电压基准的噪声水平应小于 0.27 mV_pp）；如满足该条件，则根据不相关噪声正交相加这一事实（等式 1），预期所有测量噪声一定来自 ADC。

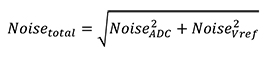[1]

如果 Noise_Vref = Noise_ADC/3，则 Noise_total = 1.054× Noise_ADC。这意味着电压基准仅占总噪声的 5.4% ，几乎可以忽略不计。如果发现电压基准的噪声超过 ADC 噪声的 1/3，牢记只需从测量标准偏差中减去其贡献值即可（见等式 2）。

[2]

如何了解电压源的噪声水平

最简单的方法是在数据表中查找。如 Texas Instruments REF5030 数据表中的数据所示，该器件的噪声水平为 9 μV_pp。

图 4：摘自 REF5030 数据表，给出了输出电压噪声规格。(图片来源：Texas Instruments）

如果数据表中没有列出噪声水平（或只是为了验证其数值），则只需用示波器测量即可，不过首先需要知道示波器的本底噪声。具体操作是将示波器的一个输入端接地，然后测量信号变化的有效值 (RMS)。如图 5 所示，使用 Analog Discovery 2 (AD2) 进行处理的结果，表明噪声 RMS 约为 0.9 mV。有趣的是，如果时基增加到 8 µs/div 以上，该值就会下降（下降到 µV 范围内），这可能是因为 AD2 使用了过采样和抽取法来提高其有效分辨率。

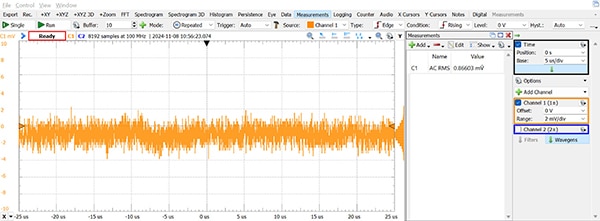图 5：Analog Discovery 2 示波器的本底噪声水平图。(图片来源：Nathan Jones）

测量电压源时，示波器信号的任何变化都是电压源和示波器中的组合噪声造成的。只要这些噪声源不相关（它们是不相关的），那么 Noise_measured = √(Noise²_Scope + Noise²_Vref) 和 Noise_Vref = √(Noise²_Measured - Noise²_Scope），即如上所述。在测量 AD2 产生的 2 V_DC 信号时，噪声被确定为 1.2 mV（图 6）。

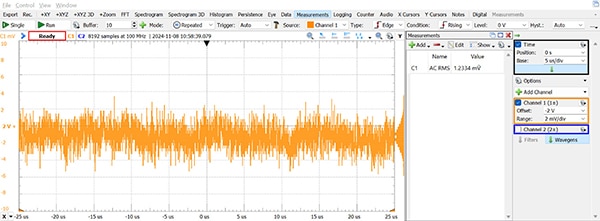图 6：这张 2 VDC 信号图显示示波器的噪声为 1.2 mV。 (图片来源：Nathan Jones）

这表明 AD2 上的信号发生器也有约 0.9 mV 的噪声水平。对于测试 10 位 ADC 来说，这个数值已经足够低了（对于满刻度读数为 3.3 V 的 10 位 ADC 来说，0.9 mV 还不到 1/3 LSB）；而对于任何更高分辨率的 ADC 来说，在测量时必须考虑这个噪声。

图 7：该插图展示了 10 万个光敏电阻电压样本在采用基准电压源时的 ADC 值新直方图。(图片来源：Nathan Jones）

这样就好多了！现在请注意，第二个直方图（图 7）的 x 轴仅到 2052（该图 [图 8]上的分布标准偏差为 1 LSB），而第一个图则达到 2100（其标准偏差为 15 LSB）。这就是所谓的 ADC DC 直方图测试，且标准偏差有效地表明了 ADC 中的噪声大小：无论何时通过 ADC 测量某个值时，模拟引脚上的真实值实际上在该值 ±1 标准偏差范围内的概率只有 68% ，但真实值在该值 ±3 标准偏差范围内的概率为 99.7% 。

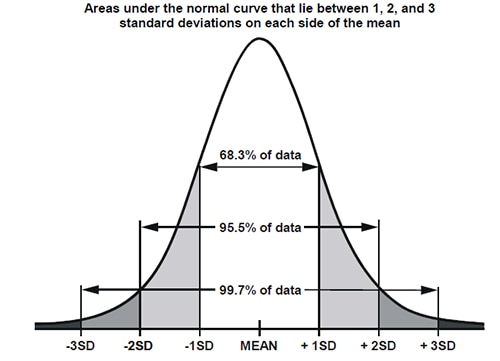图 8：带有标准偏差的分布曲线。(图片来源：https://i.sstatic.net/jkMDV.png）

将这一标准偏差从 LSB 转换为伏特，就会得到 ADC 的输入参考噪声（等式 3）。

[3]

如果 ADC 具有如此小的噪声，即所有 ADC 代码都落在一个单区间内，则可尝试降低 ADC 的基准电压。噪声水平将保持不变，但会占用比以前更多的 ADC 代码，从而可为输入参考噪声找到一个合适的值。

ADC 的有效分辨率和无噪声代码分辨率 (NFCR) 表示噪声对 ADC 分辨率的限制程度，计算方法是将全范围 ADC 代码分成宽度仅为 1 个（等式 4）或 6.6 个标准差（等式 5）的小区间。

[4]

[5]

从根本上说，结果中的实际位数会减少，这是因为 ADC 结果中最后几位出现错误或噪声的可能性越来越大。

在进行 DC 直方图测试时，一个稍微简单的方法是将 ADC 输入接地，然后创建 ADC 结果的直方图（图 9），就像使用示波器时那样。

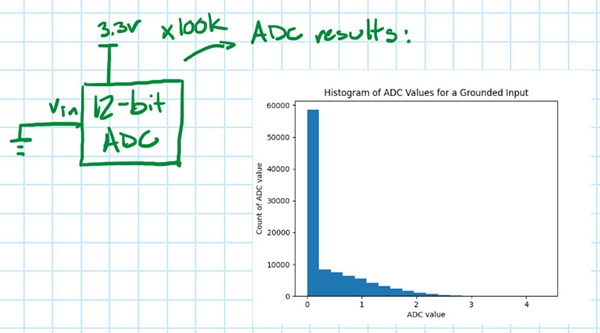图 9：插图所示为 ADC 输出电压采样的直方图，输入接地。(图片来源：Nathan Jones）

该直方图的标准偏差也是 ADC 噪声的测量值（减去 ADC 基准电压中的任何噪声，这不会影响 0 V 的读数），但标准偏差非常低。ADC 可能将小于 0 V 的值报告为 0，因此只能看到真实噪声分布的一半。在这种情况下，如果假定平均值的分布是对称的，将足够多的中值改为负数，使分布变得对称，然后计算其标准偏差，就可以近似地计算 ADC 噪声（图 10）。

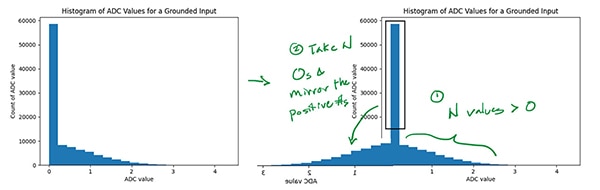图 10：图 9 直方图的镜像，可近似地求出 ADC 噪声。(图片来源：Nathan Jones）

好吧，那么该如何应对这些噪声呢？如果 ADC 的分辨率仍在项目要求范围内（幸运！），那么请记住，每个 ADC 测量值都有一定的不确定性：

• 在比较两个 ADC 值时，只有当它们的误差在 6.6 σ 以内（比较的置信度为 99.7% ）或它们的误差在 σ 以内（置信度仅为 68% ）时，才能将其视为等效。
• 将 ADC 值与阈值进行比较时，应在阈值比较中增加一些滞后（就像恒温器那样），以避免嵌入式系统在高于或低于该阈值时因噪声而重新触发。

如果发现 ADC 不符合项目要求，可以尝试一些简单的方法来提高其性能。硬件方面包括：

• 为 AVCC 和 AREF 使用低噪声基准（如 Texas Instruments 的 REF5030 或 EVVO TL431
• 确保将 PCB 上的模拟信号和数字信号之间的串扰降至最低
• 在 ADC 转换期间关闭 CPU（如果 MCU 支持该功能），以减少数字噪声

在软件方面，可以对输入信号进行过采样（即取 N 个采样点的平均值）以减少噪声，但这显然会降低最大采样率。(事实上，可以使用一种名为“过采样和去量化”的技术，通过与输入的过采样次数相关的数量来提高 ADC 分辨率！）。

假设初始设置的 DC 直方图测试标准偏差为 1 LSB。如果 ADC 读数为 2048，这 是否意味着（有 68% 的概率）真实值为 1.650±0.008V（图 11）？

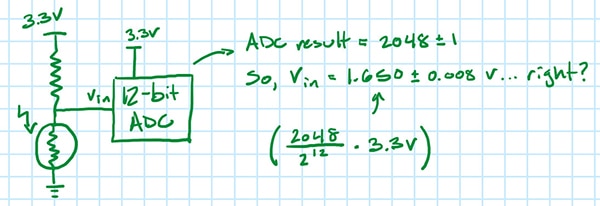图 11：假设图 1 设置的标准偏差为 1 LSB，ADC 输出为 2048，那么真实的输入电压是 1.650±0.008 V 吗？(图片来源：Nathan Jones）

比较接近，但还不是！这是因为所有 ADC 在测量某个频率上快速变化的输入信号时都会遇到困难，导致测量结果不精确（即噪声）。令人惊讶的是，发生这种情况的频率可能远远低于 ADC 的最大采样率！这意味着，采样率为 1 MSPS（百万采样/秒）的 12 位 ADC 在输入信号频率接近 500 kHz 时，分辨率实际上可能没有 12 位；当输入信号频率如此之高时，该 ADC 的分辨率可能降至 6 位或更低。如果要测量光敏电阻上高于 10 Hz 的信号，ADC 的分辨率实际上可能没有 12 位。

要确定 ADC 的分辨率在更高输入频率下的保持能力，可输入一个已知良好信号（这次是正弦波信号），然后测量 ADC 值与该已知良好信号的匹配程度（图 12）。(正弦波信号是否“足够好”？这一点将在测试过程公布后再讨论；那样会更有意义）。

图 12：使用已知的良好正弦波输入的测试设置。(图片来源：Nathan Jones）

要生成正弦波，可以使用函数发生器（如许多 USB 示波器上的函数发生器）、DDS 芯片（如 Analog Devices 的 AD9834），或者组装一个定制正弦波发生器（如基于 Wien 桥振荡器或使用 Analog Devices 的 MAX7400 对方波进行低通滤波处理）。需要注意的是，该测试中使用的输入频率只能是采样频率的 非 整数分频（例如，如果采样率为 100 kHz，则不要使用 1 kHz 输入频率）。这是为了避免在每个周期的相同位置对正弦波进行错误采样。此外，为了对 ADC 进行极限施压，应将输入正弦波的振幅设置为不会导致“削波”输出的最大值（例如，上述示例中 ADC 的振幅应略低于 1.65 V）。

收集 ADC 结果后，将数据与正弦波拟合，以计算残差。正弦波拟合几乎可以使用任意数量的数据，但要获得最佳结果，输入的正弦波必须至少有五个完整的周期。可能需要对正弦拟合算法进行初始化，给出振幅、频率、相移和偏移的初始值（图 13）。

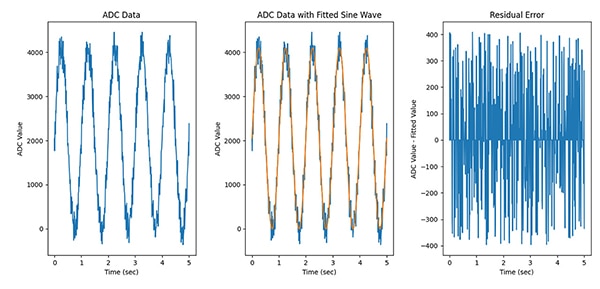图 13：使用正弦波拟合算法可以确定残差。(图片来源：Nathan Jones）

该测试称为 ADC 的正弦波拟合测试，残差的 RMS 用来衡量 ADC 在特定输入频率下的噪声程度。较低频率下，应有 RMS 噪声与 DC 直方图测试中的输入参考噪声相匹配，但在较高频率下，由于上述与频率相关的噪声源影响，RMS 噪声几乎肯定会降低。

正弦波拟合测试的 RMS 噪声值可用于计算 ADC 的有效位数 (ENOB)（等式 6），即理想 ADC 的位数，其唯一噪声源——量化噪声的 RMS 值与 ADC 中的噪声相同。

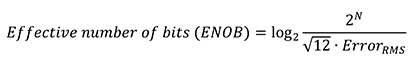[6]

该值与所用的输入信号频率有关。为了更全面地了解 ADC，应在直至相关的最高输入信号频率或最高采样率一半时的整个频率范围内，重复进行此测试。你可能会发现，当频率远低于最大采样率一半时的频率点，噪声会大大增加（而 ENOB 则会大大降低！）。例如，我们对 STMicroelectronics STM32F042K6 中的 ADC 进行了一系列精确测试，并绘制了测试结果图（图 14）。

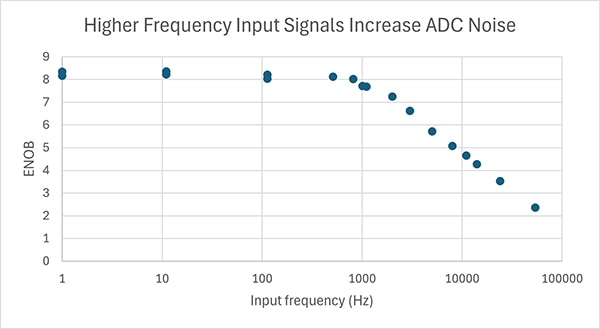图 14：STM32F042K6 微控制器中 ADC 的频率噪声测试。(图片来源：Nathan Jones）

尽管 STM32F042K6 微控制器上的 ADC 可以 1 MHz 的频率采样，但分辨率高于 1 kHz 时就会下降；如果要使用该 ADC 测量 10 kHz 的信号，那么分辨率将只有大约 5 位！(请注意，最大 ENOB 约为 8.3；这是因为即使在直流电压下也会有约 10 LSB 的噪声，这会将 ADC 的有效分辨率从 12 位直接降至约 8.7 位。这些测试是通过一块未修改的 STMicroelectronics Nucleo-F042 开发板进行的；如果使用上述任何一项技术，测试结果都会更好（“好吧，那么该如何消除这些噪声呢？）

如何知道正弦波的噪声水平

与电压基准一样，如果正弦波的噪声水平未预先提供（即数据表中没有），则需要使用示波器进行测量。使用前面讨论过的正弦波拟合技术，可以确定正弦波发生器的噪声特征。

1. 首先，将示波器的输入端接地并计算输出的 RMS（如前“如何了解 电压源的噪声水平”部分所述），从而确定示波器的本底噪声。
2. 然后，测量正弦波发生器的输出，将结果拟合为完美正弦波，并计算残差的 RMS 值。然后使用等式 2 确定正弦波发生器的噪声（使用示波器的本底噪声作为其 AC 噪声的近似值）。

理想情况下，正弦波的噪声水平应小于 ADC 预期噪声水平的 1/3（换句话说，正弦波具有“频谱纯净”特性），这将使其对测量噪声的贡献可以忽略不计。如果正弦波的噪声水平高于该值，请记住要从计算残余误差 RMS 值得到的测量噪声中减去该值。

对于要用于测试 ADC 的每个输入频率（甚至正弦波发生器也可能有与频率相关的噪声源！），都应重复进行此测试。

如何消除这些噪声？首先，建议在信号源和 ADC 之间连接一个低通滤波器 (LPF)，且其截止频率应略高于所关注的最高频率信号，以协助限制高频噪声（通常，对于任何数据采集系统来说，这都是“值得遵循的原则”）。如果所关注的最高频率信号低于 ENOB 与输入频率关系图中的“拐点”，则实际上就不会降低分辨率。在测量“拐点”以上的信号时，有几种方法可用于在较高频率下提高分辨率。具体包括：

• 确保与模拟引脚连接的设备具有低输出阻抗，可以考虑插入运算放大器进行缓冲
• 调整 ADC 时钟或其采样/保持时间，使其尽可能快，同时让内部电容仍具有足够的时间充电
• 使用低抖动 ADC 时钟源，并对系统进行，使其定期采集 ADC 样本

除非目标信号位于非常窄的频带内，否则接下来最直接的做法是，假设实际输入信号从 DC 到 LPF 截止频率之间具有相同的频率成分，因此 ADC 每次测量的 RMS 噪声就是在 DC 到截止频率范围内使用正弦波拟合测试所测得的平均 RMS 噪声。如果希望使用上文讨论过的 STM32F042K6 测量高达 10 kHz 的宽带信号，那么最好在每次测量时将 ADC 的 ENOB 设置为 6 位左右。该值很可能低于使用 DC 直方图测试确定的值，这表明如果 ADC 测量的频率成分可能较高，那么每个 ADC 测量值的确定性就会降低。

下一个需要考虑的假设是，在传感器和 ADC 之间增加一个 LPF，这样从 DC 到截止频率的 RMS 噪声仅为 ±1 LSB。如果 ADC 读数为 2048，现在 是否意味着（有 68% 的可能性）真实值为 1.650 ±0.008 V（图 15）？

图 15：在电路中添加低通滤波器后，真实值否因此稳定为 1.650±0.008 V？(图片来源：Nathan Jones）

尽管听起来很疯狂，但 目前还无法实现！虽然本文已经有很好地描述了 ADC 中的 噪声 特征，但还没有描述其 误差 的特征。通过本文所述的测试后，唯一可以确定的是两个 ADC 值相同还是不同。但 ADC 代码为 2048 时对应的是精确的 1.65 V 还是其他值，目前还不得而知。增益、偏移和差分非线性误差（以及其他误差）可能意味着，从 ADC 代码转换为实际电压比使用 V_in=ADC result × V_FS/2^N 更为复杂。不过，这不是本文要讨论的主题！

参考文献

1. 确定 Raspberry Pi Pico ADC 的特征
2. 了解数据转换器（Texas Instruments）
3. 了解 SINAD、ENOB、SNR、THD、THD + N 和 SFDR，避免迷失在本底噪声中 (Analog Devices)
4. ADC 输入噪声的“好、坏、丑的一面”——无噪声就是好噪声吗？Analog Devices
5. 充分利用 SAM D21 的模数转换器（Thea Codes）
6. “模数转换器测试”（Kent Lundberg）
7. A/D 转换器性能的动态测试（Texas Instruments）
8. 如何优化 STM32 MCU (STM) 的 ADC 精确度
9. 通过超采样提高 ADC 分辨率（Atmel）
10. 精密 ADC 噪声分析基础（Texas Instruments）
11. 基于 ARM® Cortex®-M0+ MCU 的 ADC 增益和失调误差校准 (Microchip)
12. 通过对方波进行低通滤波来产生正弦波
13. 了解数字化仪的噪声对示波器测量值的影响（EE Times）
14. 了解有效位数（Robust Circuit Design）